钱付平等：褶型空气过滤介质结构参数对其压力损失影响的规律研究

褶型空气过滤介质结构参数对其压力损失影响

的规律研究

朱景晶，钱付平^*，叶蒙蒙，魏民，韩云龙，鲁进利

（安徽工业大学 建筑工程学院 安徽 马鞍山 243032）

摘要：构建52个褶型空气过滤介质微观物理模型及6个宏观物理模型，共计设计285种工况，对褶型空气过滤介质的压力损失进行计算流体动力学（CFD）分析，探究结构参数与压力损失之间的数学关系，得到了具有实际应用价值的褶型空气过滤介质压力损失的数学模型。所得数学模型同实验数据进行对比发现，最大处误差不超过8%。同时，分析讨论了褶型空气过滤介质结构参数对内部流场的影响，结果表明孔隙率ε、褶尖角θ、褶高h等均与介质两端压力损失存在明显的数学关系；褶尖角区域在过滤过程中发挥的作用有限，但是有效过滤体积会随着褶尖角的增大而增大。褶型空气过滤介质本身存在最优结构使得压力损失最小。本研究对褶型空气过滤介质的理论研究及结构优化研究具有重要的参考价值和指导意义。

关键词：褶型空气过滤介质；压力损失；数学模型；CFD

Study on the Basic Law of Pressure drop in Pleated Air Filter Media

Jingjing Zhu, Fuping Qian, Mengmeng Ye, Min Wei, Yunlong Han, Jinli Lu

School of Civil Engineering and Architecture, Anhui University of Technology, Ma'anshan 243002, PR China

Abstract: 52 micro-physical models and 6 macro-physical models of pleated air filter media were constructed. A total of 285 working conditions were designed. Computational Fluid Dynamics (CFD) analysis of pressure drop in pleated air filtration media was carried out to explore the mathematical relationship between structural parameters and pressure drop. The mathematical model of pressure loss of pleated air filter media with practical application value is obtained. By comparing the mathematical model with the experimental data, it is found that the maximum error is less than 8%. At the same time, the influence of structural parameters of pleated air filter media on the internal flow field is analyzed and discussed. The results show that there are obvious mathematical relationships between the porosity ε, pleated angle θ, pleated height h and pressure loss. The pleated angle zone plays a limited role in the filtration process, but the effective filtration volume will increase with the increase of the pleated angle. And the pleated air filter media itself has an optimal structure to minimize pressure loss. This study has important reference value and guiding significance for theoretical research and structural optimization of pleated air filter media.

Key words: Pleated air filter media; Pressure drop; Mathematical model; CFD

1前言

褶型空气过滤介质相对于平板型过滤介质来说过滤面积更大、过滤效率更高、所占空间更小，但是，其内部流场也更加复杂。因此，平板型空气过滤介质的研究相对已经成熟，而对于褶型空气过滤介质来说，具有直接利用价值的研究成果相对较少。在褶型空气过滤介质研究的早期，研究者会基于单纤维理论对压力损失展开研究。早在1959年，Kuwabara 和Happel ^[1,2]就采用胞壳模型对单纤维过滤性能进行了预测，获得可被接受的预测值，认为气流函数可以用斯托克斯近似值来表示。1856年法国工程师Darcy提出了著名的达西定律^[3]，有研究者将达西定律应用在空气过滤介质研究当中。在达西定律的应用过程中，无量纲压力损失关联式成为研究者们关注的重点。Davies^[4]提出了预测平板型空气过滤介质无量纲压力损失的重要关联式。Banks^[5]则基于Davies的研究成果，结合单纤维理论，考虑了纤维轴向与气流方向的夹角（非零），将达西定律成功的引入到褶型空气过滤介质的研究当中，得出应用范围更广的无量纲压力表达式，可用于洁净过滤阶段褶型空气过滤介质的压力损失计算。目前，褶型空气过滤介质的理论研究仍在继续，研究者们致力于简化数学模型形式，研究重点转移到褶型空气过滤介质结构参数与压力损失的关系上来。Fabbro等^[6]得到了由结构参数构成的表达式。付海明等^[7]通过理论分析认为压力损失可以拆分计算。查文娟等^[8]基于响应曲面法分析了不同褶高、褶间距和过滤风速对褶式滤芯阻力的影响并得到预测模型。Saleh等^[9]通过对褶型空气过滤介质的结构分析，导出关于压力损失的表达式，可用于褶型空气过滤介质的结构设计。Félicie等^[10]研究了不同的褶结构对纤维表面速度场的影响，进而分析了褶的结构参数对压力损失的影响。Li等^[11]则对褶型空气过滤介质的有效过滤面积进行了讨论，并力求建立一个有效的数学模型来描述褶的结构参数与压力损失之间的关系。

目前，褶型空气过滤介质因其结构及流场较为复杂，理论研究成果太过繁杂，实用性不强。同时，由于实验的局限性，褶型空气过滤介质内部流动机理研究成果不多，关于其结构的优化大多只是停留在宏观层面，如褶高与褶开口距的比例优化、褶数的优化等^[12-15]。本研究通过对褶型空气过滤介质的多尺度研究，研究洁净过滤状态下介质主要结构参数与压力损失之间的数学关系，力求得到一个具有实际应用价值的数学模型。通过对微观尺度下褶型空气过滤介质内部流场的分析，提出了有效过滤体积的概念来解释褶型空气过滤介质的宏观表现，并借此为褶型空气介质的结构优化与应用提供理论支持和指导。 

2 褶型过滤介质的经验理论及数值计算

2.1 达西定律

达西定律（Darcy's law）^[3]可用于描述低速层流状态下流体流经多孔介质时渗流速度与压力损失之间的关系，又称线性渗流定律。1856年由法国工程师达西通过实验总结得到。目前，工程界普遍认为达西定律只适用层流状态流体，而本研究中所有工况均属于层流，因此可以依据达西定律进行相关研究。1852-1855年，达西进行了水通过饱和砂的实验研究，发现了渗流量Q与上下游水头差（h₂- h₁）和垂直于水流方向的截面积A成正比，而与渗流厚度t成反比关系，即：

2.2 数值计算

本研究为确定褶型空气过滤介质各参数与压力损失之间的数学关系，建立了微米尺度的微观拟态化模型；为将数学关系推广至宏观尺度，同时还建立了宏观尺度的数值计算模型。

微观尺度层面，为了使建立的模型更加接近真实纤维滤料的结构，本研究结合编程软件Matlab与CFD前处理软件重建出褶型空气维过滤介质的三维微观拟态化模型，如图1（a），（b）所示^[17]，重建的三维模型与真实滤料结构相似，从而为基于微观结构模拟计算纤维过滤介质的过滤性能奠定了重要基础。

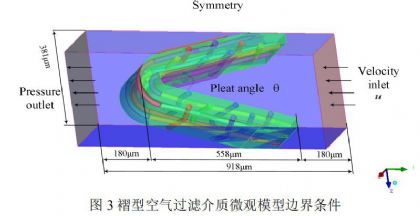
因为微尺度物理模型结构尺寸相对于宏观尺度结构来说相差100倍以上，因此可以认为微观尺度物理模型为宏观尺度模型的一个体积单元。 为研究褶型空气过滤介质结构参数与压力损失之间的关系，在洁净过滤阶段对微米尺度的微观拟态化模型进行CFD计算。计算模型区域示意图及部分相关尺寸如图3所示。为保证进出口断面气流的均匀性，计算域上下游长度各取100µm的流体区域；计算区域四周的边界则根据纤维滤料结构特点设为对称边界条件；纤维表面边界设置为无滑移固壁边界条件； 本次研究参考实际情况，以褶型空气过滤介质的褶尖角θ（1°、5°、10°、15°、20°、25°、30°、35°、40°、45°、50°、55°、60°）与孔隙率ε（75%、80%、85%、90%） 为变量，共建立52个微观模型，改变迎面风速u（0.4m/s、0.6 m/s、0.8 m/s、1.0 m/s、1.2 m/s）对上述52个模型在洁净过滤状态下进行仿真模拟，共计13×4×5=260种工况，研究不同结构条件下迎面风速与介质两端压力损失之间的关系。

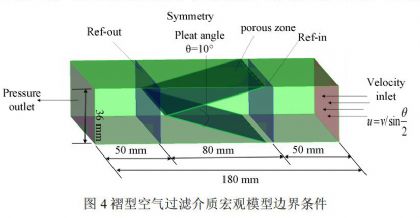
为研究介质体积对两端压力损失的影响，在洁净过滤阶段对宏观尺度的结构模型进行CFD模拟。计算模型区域示意图及部分相关尺寸如图4所示。为保证进出口断面气流的均匀性，计算域上下游长度各取50mm的流体区域；计算区域四周的边界则根据褶型滤料结构特点设为对称边界条件；过滤介质内部设为多孔区域（porous zone）模型。

本次研究参考实际工程情况，以褶型空气过滤介质的褶高h（20mm、40mm、60mm、80mm、100mm）为变量，其它结构参数保持一致，共计建立5个宏观模型，改变迎面风速u（0.4m/s、0.6 m/s、0.8 m/s、1.0 m/s、1.2 m/s）对上述5个模型在洁净过滤状态下进行数值模拟，共计25种工况，研究不同褶高条件下迎面风速与介质两端压力损失之间的关系。

3 分析与讨论

3.1压力损失数学模型

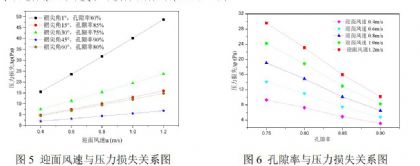
通过微观尺度模拟，采用控制变量法对得到的260组数据进行分析，发现各结构参数对过滤介质的压力损失都有着较为明显的数学关系。在低速条件下，压力损失随着迎面风速的增加而线性增加，改变介质孔隙率得到了一致的结论，如图5所示。并且低速条件下，介质孔隙率与压力损失也呈现较为明显的线性关系，压力损失随孔隙率的增大而减小，以褶尖角为15°时的模型为例，数据趋势如图6所示。压力损失与孔隙率的线性关系证明本研究取局部纤维进行拟态化建模，进行周期性研究是合理的。

基于1stopt软件处理上述260组数据由微观尺度模拟的得到的数据，以合适的公式形式，采用麦夸特法（Levenberg-Marquardt） 和通用全局法对数学模型进行优化得到褶型空气过滤介质洁净过滤状态下单位体积内的压力损失计算公式：

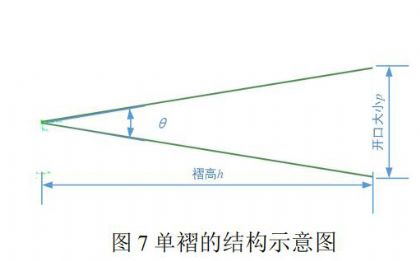
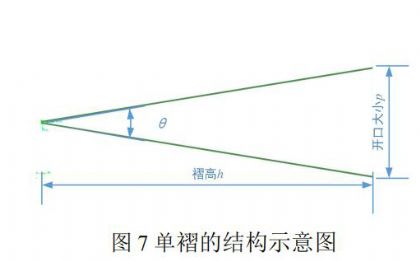
褶型空气过滤介质在褶尖角θ和褶厚t确定的前提下，褶高h可以决定整个褶型空气过滤介质的体积。因此，数学关系向宏观尺度的推广，即确定体积V对压力损失的影响研究可以转化为褶高h与介质两端压力损失之间的关系研究。宏观尺度仿真结果表明，在迎面风速一定的情况下，随着褶高的增加，压力损失先增大后减小，之后趋于稳定，稳定阶段会有不明显的增长趋势，并且压力损失存在一个明显的峰值。迎面风速越大，此现象表现越为明显，如图7所示。上述现象存在的原因是当褶尖角θ、褶厚t以及迎面风速u一定时，褶高h会影响褶的开口距p，进而基于式（2）影响到断面流量Q，即随着褶高的增加，断面流量Q不断增大。但是，随着褶高的增加，有效过滤面积也会不断增大。前者会使得压力损失增加，而后者则会导致压力损失减小。当褶高h相对较小时，有效过滤面积集中在开口段，变化不是特别明显，但是因为褶高h相对较小，介质内部流体活动空间相对狭小，断面流量Q对压力损失产生较大的影响。因此这一阶段断面流量Q对压力损失的变化起主导作用，会使得压力损失逐渐增大。当褶高h增加到一定值时，随着褶高的增加，介质内部流体活动空间不断扩大，有效过滤面积也会明显增加，并且随着褶高h的增加，气流的速度受阻力影响会表现明显，气流的动能会随之衰减。此时，有效过滤面积对压力损失变化的影响逐渐占据主导，因此导致压力损失在达到峰值后逐渐减小。最后，当有效过滤面积趋于稳定后，压力损失变化趋于稳定，但是受断面流量Q及气流长距离动能衰减等多因素综合影响，压力损失变化呈现稳中有升的现象。上述有效过滤面积是指过滤介质中可以有效过滤的部分面积的总和，本研究中具体表现为有效阻止气流通过的部分的面积。宏观尺度有效过滤面积概念对应后文微尺度研究中的有效过滤体积概念，将在后文做相应介绍。

其中褶高h与褶尖角θ对压力损失的共同影响即为体积V对压力损失影响的数学体现。上述数学模型与公式（8）保持一致，证明本文得到的数学模型具有理论依据。

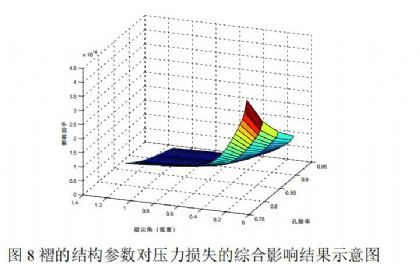
褶型空气过滤介质结构参数对压力损失值具有很大的影响，近年来关于褶型空气过滤介质的研究文献^[9-11]大多都会提及孔隙率与褶的高宽比对介质过滤性能的影响，褶的高宽比即褶高h与褶的开口距p的比值，如图8所示。实际上褶高h与褶的开口距p的比值即为褶尖角的另一种形式的体现，如式（17）所示。因此，关于褶的结构优化可以直接以孔隙率与褶尖角对压力损失的综合影响来表示。

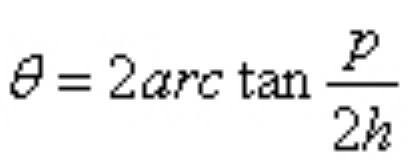
基于本研究得到的数学模型式（14）可以看出，f (α)与f (θ)的乘积与压力损失之间呈现正比关系，因此，孔隙率与褶尖角对压力损失的综合影响的研究可以转化为f(α)与f(θ)乘积的变化规律研究。此处定义：

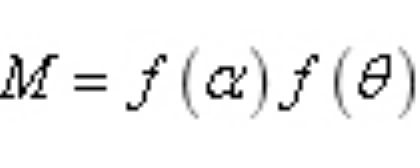
M为孔隙率与褶尖角对压力损失的综合影响因子，M值越大说明孔隙率与褶尖角对压力损失的综合影响越明显，压力损失越大。

基于本研究得到的数学模型式（14），利用Matlab软件对M进行数学分析，结果如图8所示。研究发现，随着褶尖角和孔隙率的增大，孔隙率与褶尖角对压力损失的综合影响逐渐减弱，最终褶尖角和孔隙率对压力损失的贡献将趋于稳定。具体表现为在小角度、低孔隙率的结构条件下，介质两端的压力损失最大，但是随着褶尖角和孔隙率的增大，压力损失会明显减小，最终会趋于稳定。基于图8分析，当褶尖角在0.5到0.7（弧度值）之间，即约30°到40°之间时，压力损失会趋于稳定，即在此区间内，褶型空气过滤介质结构会达到最优值。

3.2数学模型可靠性验证

为验证仿真数据及数学模型的可靠性，将数学模型计算结果与实验数据^[18] 进行对比，实验工况如表1所示，改变迎面风速u（0.5m/s，1.0m/s，1.5m/s，2.0m/s）进行仿真及实验，褶尖角基于式（17）利用褶高h及褶开口距p表示。对比结果如图9所示。

表1 实验工况

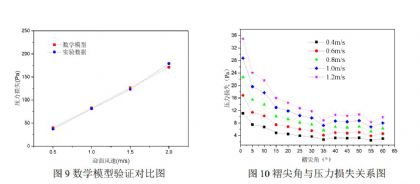
 通过对比发现，本研究得到的数学模型计算结果与实验数据基本重合，最大处误差不超过8%；因此，可以认为本研究中得到的数学模型真实、可靠，具有实用和推广价值。

上述验证过程中，实验条件已经超越了层流状态，进入过度阶段或紊流阶段。事实证明，本文得到的数学模型可以有效应用在褶型空气过滤介质层流阶段及过渡阶段的研究中。

3.3流场分析

 基于微观尺度仿真结果发现，孔隙率相同的情况下，压力损失随褶尖角的增大先减小后趋于平缓。以孔隙率为85%时的工况为例，结果如图10所示。

针对上述现象，本研究对褶型空气过滤介质的内部流场做出定量分析。以下是在不同褶尖角（其它结构参数保持不变）情况下的压力分布云图。

                          图11不同褶尖角结构下微观尺度压力云图
 

通过图11分析发现，小角度时，压力损失有着明显的阶梯式分布，褶型空气过滤介质的压力损失主要是由褶开口段区域的纤维集合造成的。并且小角度时，褶尖角区域几乎没有压力损失，甚至压力损失值出现负值。随着褶尖角角度的增加，特别是褶尖角在35°之后，开口段区域压力损失值分布趋向均匀，褶尖角区域也开始出现压力损失分布。这说明褶尖角在35°之后，褶型空气过滤介质的内部气流组织与压力分布更加合理，纤维集合发挥的作用趋向最大化，即从压力分布角度分析，褶型空气过滤介质最优角度出现在35°左右。

但是即使是在大角度工况下，相比于开口段区域，褶尖角区域对介质整体的压力损失影响仍然是比较小的，即褶尖角区域纤维集合的利用效率相对较低。基于上述现象，本研究进一步对通过褶型空气过滤介质内部气流速度分布作出分析，图12所示为在迎面风速为0.6m/s时纤维内部的速度分布情况。

 

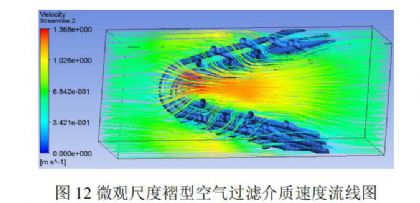
研究发现，褶尖角区域的气流速度明显高于褶开口段区域的速度，并且流场内部气流有向褶的两边纤维集合区域行进的趋势。这说明褶开口段区域相的纤维集合相对于褶尖角区域来说更加有效地阻止了气流的通过，降低了气流的动能。

因此，结合图11及图12发现，褶尖角区域相对于褶开口段区域来说其利用效率相对较低。因此，提高褶尖角区域的利用效率将会对增大褶型空气过滤介质过滤体积，减小压力损失，提高过滤效率有着积极的实际意义。

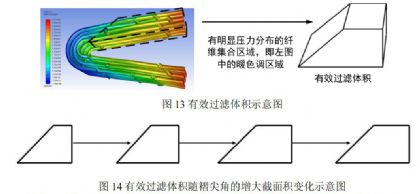
气流经过褶型空气过滤介质时，介质两边的纤维集合会产生一个有效阻止气流的区域，即从三维空间上来说因气流作用而产生压力的部分，此处可定义为有效过滤体积，如图13所示。有效过滤体积的截面积为类似直角梯形的形状。随着褶尖角的增大，直角梯形的上底边和下底边会不断向褶角处延伸，导致有效过滤体积不断增大。当褶尖角增加到一定程度时，有效过滤体积的变化则会趋于稳定。其截面的变化如下图14所示。有效过滤体积变化的宏观表现即为有效过滤面积的变化^[11]。

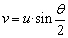
但是在小角度时，有效过滤体积对介质两端压力损失的影响大于过滤风速v的影响，占据主导地位，因此在图10中表现为压力损失值逐渐减小。

当褶角大于35°时，介质的有效过滤体积将会趋于稳定。但是随着褶角的增大，过滤风速仍然会有不明显的增长，因此在图10中表现为压力损失曲线稳中有升。

基于上述分析，因压力损失相对于孔隙率及迎面风速均为线性变化，而褶尖角对于压力损失来说存在最优解，因此洁净过滤状态下，褶型空气过滤介质结构存在最优褶角。通过分析本研究得到的最优褶角在35°左右，该值验证了前文数学模型得到的最优褶角在30°到40°之间的结论，同时最优褶角的存在也证明宏观层面褶型空气过滤介质的褶高与开口大小存在最优比例。

4 结论

本研究基于计算流体动力学对褶型空气过滤介质展开多尺度研究，分析了褶型空气过滤介质内部流场规律，得到以下结论：

（1）总结了褶型空气过滤介质洁净过滤阶段压力损失数学模型，与实验数据对比发现本研究总结的数学模型真实、可靠，具有实际应用价值；

（2）褶型空气过滤介质结构参数与压力损失之间均存在数学关系。压力损失会随着迎面风速的增加而线性增加；会随孔隙率的增大而线性减小；会随着褶高的增加，先增大后减小，之后趋于稳定。综合以上因素判断，褶型空气过滤介质存在最优结构使得压力损失最小。

（3）褶尖角区域对褶型空气过滤介质来说利用效率较低，因此如何提高褶尖角区域的利用效率对褶型空气过滤介质的结构优化具有重要意义。

（4）在褶尖角较小的情况下，褶尖角引起的有效过滤体积的变化对压力损失的影响占据主导地位。但是随着褶尖角的增加，有效过滤体积趋于稳定，多因素综合作用下褶型空气过滤介质压力损失值趋于稳定。

参考文献

[1] Kuwabara S. The forces experienced by randomly distributed parallel circular cylinders of spheres in a viscous flow at small Reynolds number [J]. Journal of the Physical Society of Japan, 1959, 14 (4): 527-532.

[2] Happel J. Viscous flow relative to arrays of cylinders [J]. AIChE Journal, 1959, 5 (2):174-177.

[3] Bear J. Dynamics of fluids in porous media [J]. Engineering Geology, 1972, 7(2):174-175.

[4] Davies C N. Air Filtration [M]. London: Academic Press, 1973. 47(1):267.

[5] Banks D O. Stokes flow through a system of parallel infinite cylinders with Aaxes Ooriented at angle to the direction of mean flow [J]. Particulate Sci. Technol., 1987, 5(3): 339−353.

[6] Fabbro L D, Laborde J C, Merlin P, et al. Air flows and pressure drop modeling for different pleated industrial filters [J]. Filtration & Separation, 2002, 39(1):34-40.

[7] 付海明, 徐芳, 晋瑞芳. 褶型气溶胶过滤器过滤阻力与结构参数关系[J]. 华侨大学学报(自然科学版), 2010, 31(3):307-312.

[8] 査文娟, 钱付平, 鲁进利,等. 基于阻力的V型褶式滤芯结构参数的响应面法优化[J]. 过程工程学报, 2013, 13(5):771-775.

[9] A.M. Saleh, H. Vahedi Tafreshi, B. Pourdeyhimi et al. An analytical approach to predict pressure drop and collection efficiency of dust-load pleated filters [J]. Separation and Purification Technology，2016, 166:80-87.

[10] Théron F, Joubert A, Coq L L. Numerical and experimental investigations of the influence of the pleat geometry on fibrous filter performances for submicronic aerosol depth filtration [J]. Separation & Purification Technology, 2017, 182:69-77.

[11] Li S , Hu S , Xie B, et al. Influence of pleat geometry on the filtration and cleaning characteristics of filter media[J]. Separation and Purification Technology, 2018, 210:38-47.

[12] 袁惠新, 刘明爽, 吕浪,等. 褶型筒式空气过滤器过滤压降的数值模拟[J]. 环境工程学报, 2017, 11(5): 2946-2950.

[13] Chen S W, Wang Q, Chen D R. Effect of pleat shape on reverse pulsed-jet cleaning of filter cartridges [J]. Powder Technology, 2017, 305(2017): 1-11.

[14] Chen S W, Chen D R. Annular-slit nozzles for reverse flow cleaning of pleated filter cartridges [J]. Separation & Purification Technology, 2016, 177(28): 182-191.

[15] Théron F, Joubert A, Coq L L. Numerical and experimental investigations of the influence of the pleat geometry on the pressure drop and velocity field of a pleated fibrous filter [J]. Separation & Purification Technology, 2017, 182(2017):69-77.

[16] 邓彩华, 童亮, 陈壁峰, 等. 多孔介质流动的直接数值模拟[J]. 武汉理工大学学报(交通科学与工程版), 2011, 35(6):1257-1260.

[17] 黄乃金, 钱付平, 查文娟,等. 基于微观结构的褶式滤芯拟态化模型及其过滤性能的数值模拟[J]. 过程工程学报, 2014, 14(3):402-408.

[18] Tronville P, Sala R. Minimization of Resistance in Pleated-Media Air Filter Designs: Empirical and CFD Approaches [J]. HVAC&R Research, 2003, 9(1):95-106